Manopt

Wel­come to Manopt!

Tool­boxes for opti­mization on manifolds and matrices

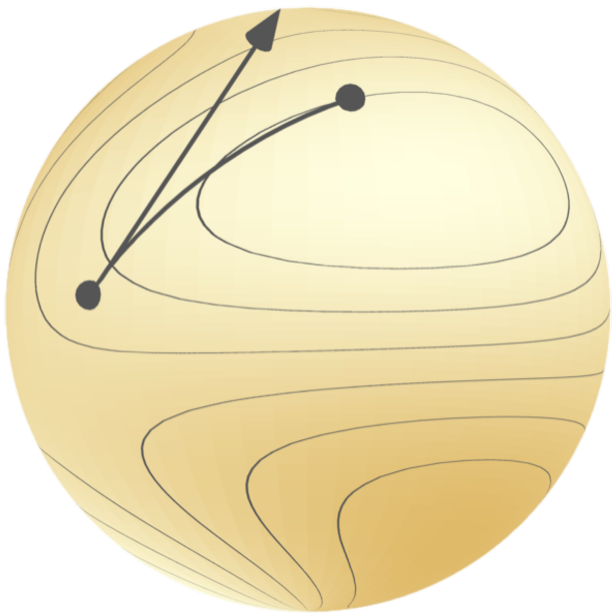
Optimization on manifolds is a powerful paradigm to address continuous optimization problems.

With Manopt, it is easy to deal with various types of constraints and symmetries which arise naturally in applications, such as orthonormality, low rank, positivity and invariance under group actions.

These tools are also perfectly suited for unconstrained optimization over vectors and matrices.

Matlab

This website is the home of the Matlab version of Manopt. Check out the tutorial, our downloads and, for the most up-to-date code, our GitHub repository.

Python

The PyManopt website houses the Python version of Manopt and its documentation. Also check out the GitHub repository.

Julia

The Manopt.jl website hosts the Julia version of Manopt and its documentation. Also check out the GitHub repository for Manopt.jl and the sister project Manifolds.jl.

Manifolds and matrices

Manifolds are mathematical sets with a smooth geometry, such as spheres. If you are facing a possibly non-convex optimization problem with nice-looking constraints, symmetries or invariance properties, Manopt may just be the tool for you. Check out the man­i­folds lib­rary to find out! Moreover, since linear spaces are manifolds, Manopt is especially convenient for optimization over matrices.

Resources

Manopt comes with a large library of manifolds and ready-to-use Riemannian optimization algorithms. It is well documented and includes diagnostics tools to help you get started quickly with barely any prerequisites in optimization and geometry. Feel free to ask questions on the forum. To learn more about the mathematical foundations, see the two books and other resources linked on the about page.

It's open source

Let us know how you use Manopt, and tell us about bugs or missing features by opening issues on our GitHub pages. Please cite the toolbox according to the language you use: Matlab, Python, Julia (click for BibTex).